编写一个函数，输入是一个无符号整数，返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

循环和位移动

这个方法比较直接。我们遍历数字的 32 位。如果最后一位是 1 ，将计数器加一，然后数字右移。
任何数字和 掩码1 进行按位与运算，可以让我们获得最后一位数字，检查下一位时，掩码左移或者参数右移。

public int hammingWeight(int n) {
    int bits = 0;
    int mask = 1;
    for (int i = 0; i < 32; i++) {
        if ((n & mask) != 0) {
            bits++;
        }
        mask <<= 1;
    }
    return bits;
}

位移动的小技巧

我们可以把前面的算法进行优化。我们不再检查数字的每一个位，而是不断把数字最后一个 1 反转，并把答案加一。当数字变成 0 的时候，我们就知道它没有 1 的位了，此时返回答案。
这里关键的想法是对于任意数字n，将 n 和 n-1 做与运算，会把最后一个 1 的位变成 0 。为什么？考虑 n 和 n−1 的二进制表示。

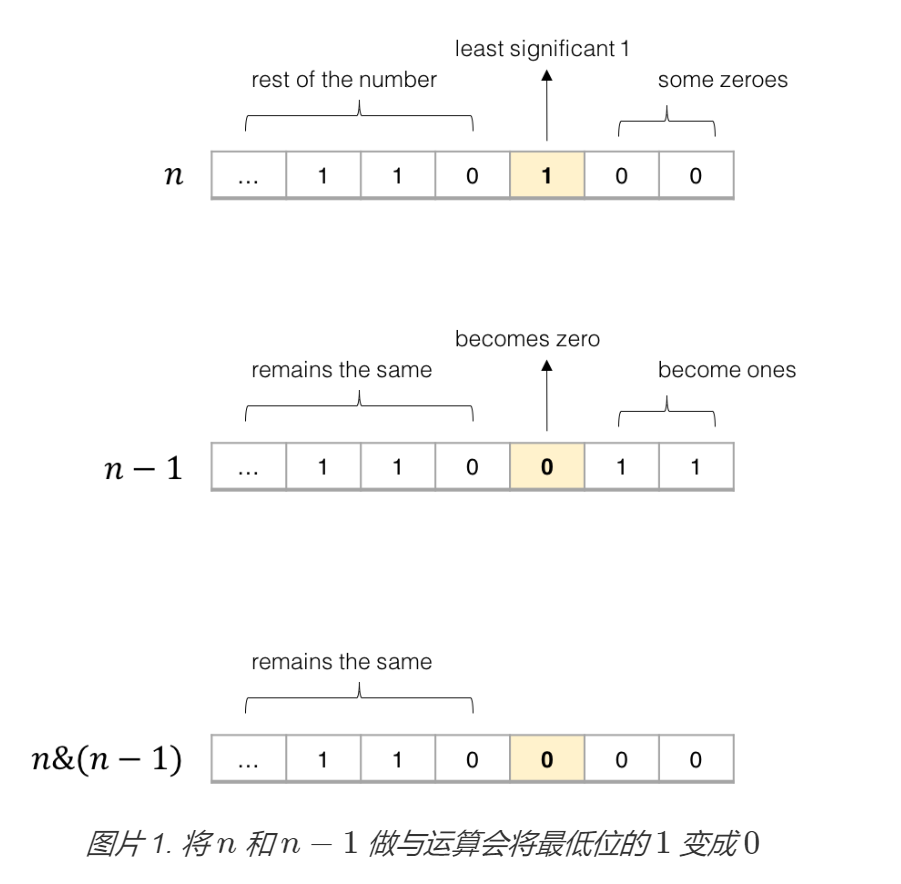
在二进制表示中，数字 n 中最低位的 1 总是对应 n−1 中的 0 。因此，将 n 和 n−1 与运算总是能把 n 中最低位的 1 变成 0 ，并保持其他位不变。

之前学到，可以利用这个判断一个数是不是2的整次幂，如果是2的整次幂，则 最低位为1 的就是 最高位 ，因此 n&n-1就会得到0

public int hammingWeight(int n) {
    int sum = 0;
    while (n != 0) {
        sum++;
        n &= (n - 1);
    }
    return sum;
}